Sin, Cos, and Tan

Help Requests
1

Hello. I’m not in trigonometry. Just want to make that clear. I also do not care. I need someone to explain Sin, Cos, and Tan, and how the hell they make the stuff rotate in Focus 2.

1 Like
2

This question doesn’t make sense. You say you want to make it clear that don’t care about Trigonometry, then ask how to to make stuff rotate with sin, cos, and & tan. The answer is Trigonometry.

So which is it?

A) You want to hear about how sin, cos, & tan work and are useful.

or

B) You don’t care to learn about Trig.

You can only choose one :thinking:

5 Likes
3

There’s a ton of uses for Trigonometry, but I can’t explain it if you don’t care.

5 Likes
4

I’m interested in this. Right now, I only know about sine & cosine waves, but I’m not sure those apply. Could someone provide insight on this?

6 Likes
5

I don’t care that I’m not in trig :laughing:
Yes, I’m eager to learn this, even tho I’m having to learn Geometry and Algebra RN :slight_smile:

1 Like
6

Its late, so I’ll try to explain more later.
But here is a Gif that really helped me, as well as a test I made.

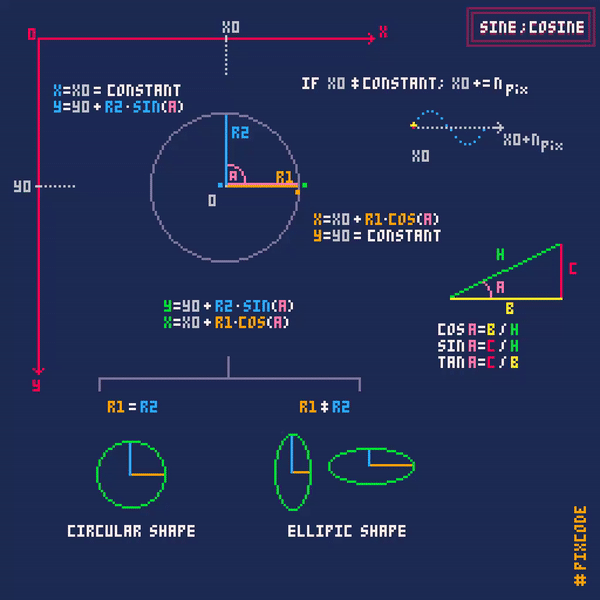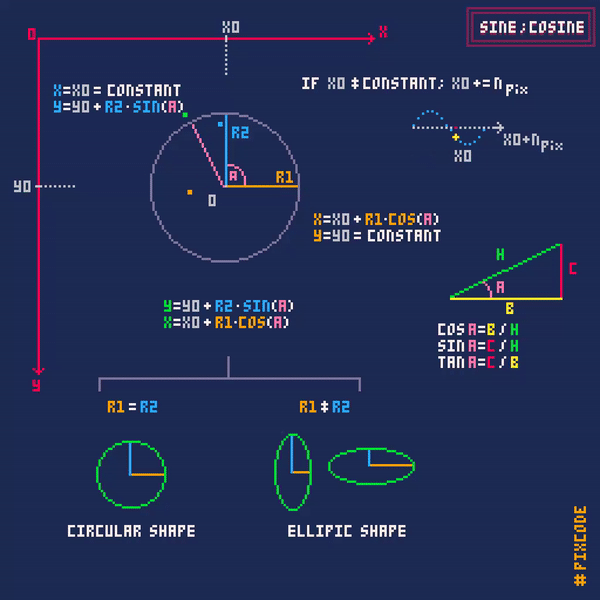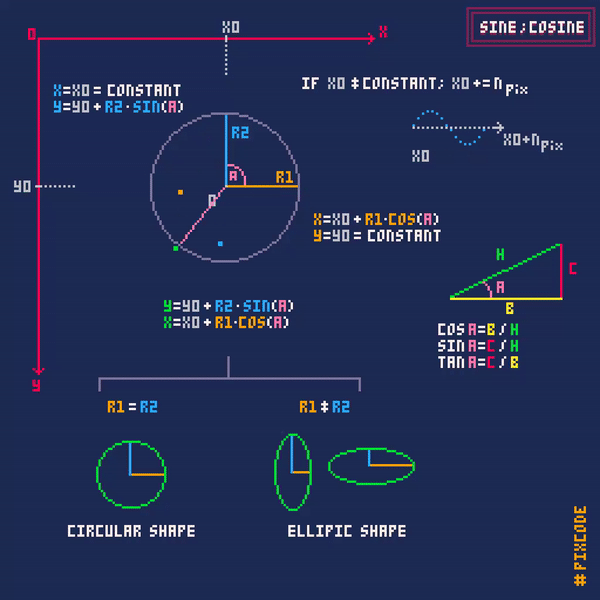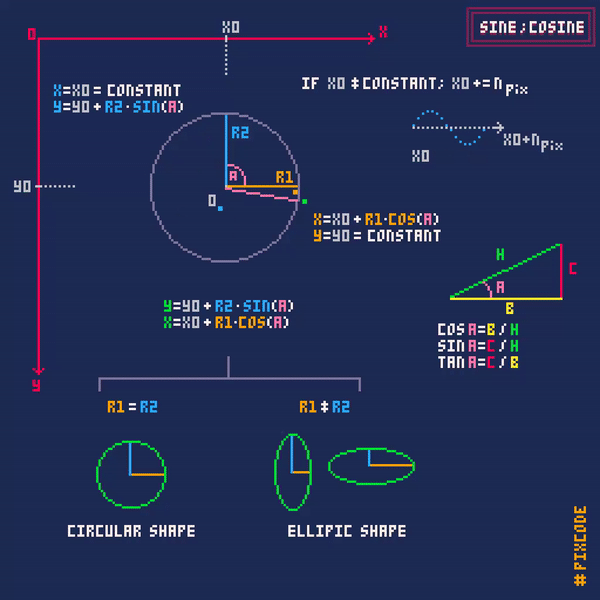
ezgif.com-gif-maker

6 Likes
7

You are close :slight_smile:
Next step is to combine those sine and cosine waves and … Tada … you get circular movements.
The example @JR01 posted is just the best :slight_smile:

5 Likes
8

Second question: how to write in the flowlab expression?

9

Ok, got that solved.
@TinkerSmith, @JR01 how would I anchor the moving object to a certain place?

1 Like
10

Nvm, just found that I need to adjust the A and stuff like that…

1 Like
11

Add the locations at the end, after all the math.

Math in the expression uses commands like Math.cos(), these commands can be found in my bundle library.

2 Likes
12

I extracted some of the expressions from your example, and found that if I adjusted the A in the evaluation I could anchor it to a location (I’m assuming that would be the Tangent), and then use the Cosine and Sine to rotate it.

13

A is added after the math like A + (other math).

And no, Tangent is its own graph. Cos plots the circle in the x axis and sin plots the points on the circles y axis. Your adding the Center of the object (X,Y) after the X and Y plots of the circle is made.

In my example, you can see the Sin and Cos lines on the axis, the ball is combining both axis

3 Likes